I-polarization ingenye yezimpawu eziyisisekelo zama-antenna. Okokuqala sidinga ukuqonda i-polarization yamaza endiza. Ngemuva kwalokho singaxoxa ngezinhlobo eziyinhloko ze-antenna polarization.
i-polarization yomugqa
Sizoqala ukuqonda i-polarization yendiza ye-electromagnetic wave.
I-planar electromagnetic wave (EM) inezici ezimbalwa. Okokuqala ukuthi amandla ahamba ngendlela eyodwa (ayikho insimu eguqukayo eziqondisweni ezimbili ze-orthogonal). Okwesibili, inkambu kagesi kanye ne-magnetic field i-perpendicular komunye nomunye futhi i-orthogonal komunye nomunye. Izinkambu zikagesi nezikazibuthe zincikene nesiqondiso sokusakazeka kwamagagasi endiza. Njengesibonelo, cabangela inkambu kagesi yefrikhwensi eyodwa (inkambu ka-E) enikezwe isibalo (1). Inkambu kazibuthe ihamba ngendlela ethi +z. Inkambu kagesi iqondiswe ku-+x. Inkambu kazibuthe ibheke +y.
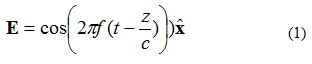
Esilinganisweni (1), bheka okuphawuliwe: . Lena ivekhtha yeyunithi (ivekhtha yobude), ethi indawo kagesi ibheke ku-x. Igagasi lendiza liboniswe kuMfanekiso 1.
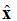
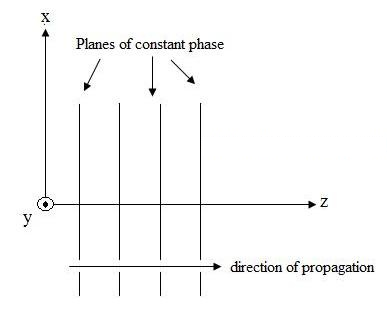
umfanekiso 1. Ukumelwa kwesithombe senkambu kagesi ehamba ngendlela ethi +z.
I-polarization yindlela yokulandela kanye nokusabalalisa (ikhonsathi) yenkundla kagesi. Njengesibonelo, cabangela i-equation yensimu kagesi ezungeza indiza (1). Sizobheka indawo lapho inkambu kagesi iku (X,Y,Z) = (0,0,0) njengomsebenzi wesikhathi. I-amplitude yale nsimu ihlelwe ku-Figure 2, ngezikhathi eziningana ngesikhathi. Inkambu inyakaza ngo-"F".
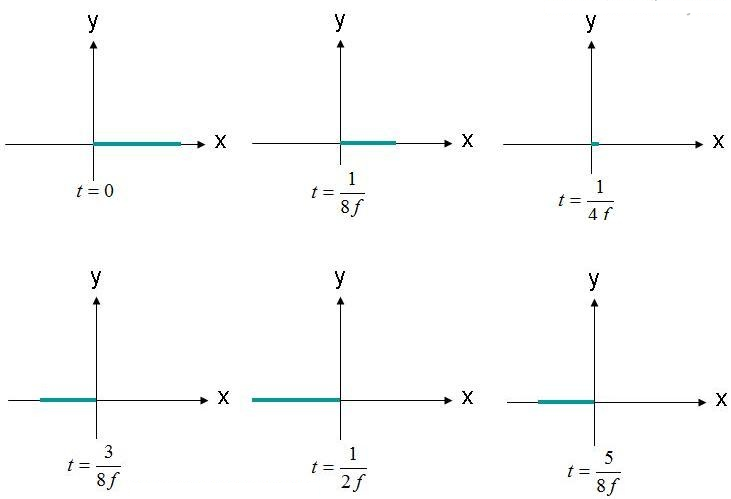
umfanekiso 2. Qaphela inkambu kagesi (X, Y, Z) = (0,0,0) ngezikhathi ezahlukene.
Inkambu kagesi ibonwa lapho isuka khona, ihlehla iye phambili naphambili ngama-amplitude. Inkambu kagesi ihlezi ihambisana ne-x-eksisi ekhonjiwe. Njengoba insimu kagesi igcinwa emgqeni owodwa, le nkambu kungathiwa i-polarized linearly. Ukwengeza, uma i-X-eksisi ihambisana nomhlabathi, le nkambu ibuye ichazwe njenge-polarized evundlile. Uma inkambu iqondiswe eduze kwe-eksisi ye-Y, igagasi kungathiwa lenziwe i-polarized mpo.
Amagagasi ahlukanisiwe aqondile awadingi ukuqondiswa ku-eksisi evundlile noma eqondile. Isibonelo, igagasi lenkundla kagesi elinesivimbelo esilele eduze komugqa njengoba kuboniswe kuMfanekiso 3 nalo lizohlukaniswa ngokwemigqa.
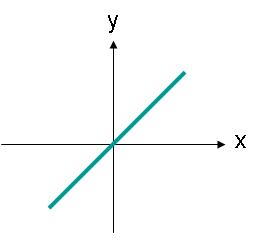
isithombe 3. I-amplitude yenkundla kagesi yegagasi elihlukanisiwe elinomugqa lapho umzila wayo uyi-engeli.
Inkambu kagesi kuMfanekiso 3 ingachazwa nge-equation (2). Manje kunengxenye ethi x kanye no-y yenkundla kagesi. Zombili izingxenye ziyalingana ngosayizi.
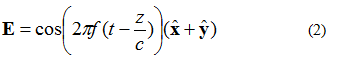
Into eyodwa okumele uyiqaphele mayelana ne-equation (2) ingxenye ye-xy kanye nezinkambu ze-elekthronikhi esigabeni sesibili. Lokhu kusho ukuthi zombili izingxenye zine-amplitude efanayo ngaso sonke isikhathi.
i-polarization eyindilinga
Manje cabanga ukuthi indawo kagesi yegagasi lendiza inikezwa nge-equation (3):
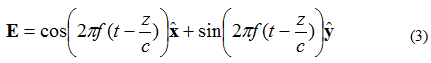
Kulokhu, ama-X- kanye no-Y-elementi angama-degree angama-90 ngaphandle kwesigaba. Uma inkambu ibhekwa njenge (X, Y, Z) = (0,0,0) futhi njengangaphambili, inkambu kagesi uma iqhathaniswa nejika lesikhathi izovela njengoba kuboniswe ngezansi kuMfanekiso 4.
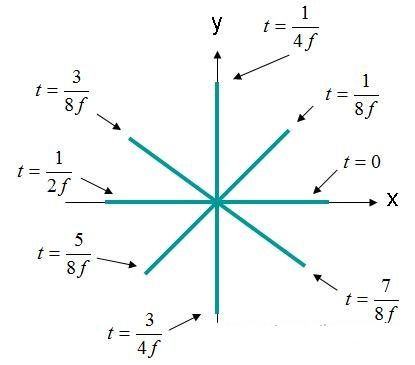
Umfanekiso 4. Amandla enkundla kagesi (X, Y, Z) = (0,0,0) isizinda se-EQ. (3).
Inkambu kagesi kuMfanekiso 4 izungeza isiyingi. Lolu hlobo lwensimu luchazwa njengegagasi eliyindilinga elihlukanisiwe. Ukuze kuhlanganiswe i-circular polarization, lezi zindlela ezilandelayo kufanele zihlangabezane nazo:
- Okujwayelekile kwe-polarization eyindilinga
- Inkambu kagesi kumele ibe nezingxenye ezimbili ze-orthogonal (perpendicular).
- Izingxenye ze-orthogonal zensimu kagesi kumele zibe nama-amplitudes alinganayo.
- Izingxenye zequadrature kufanele zibe ngama-degree angama-90 ngaphandle kwesigaba.
Uma uhamba ngesikrini se-Wave Figure 4, ukuzungezisa kwenkambu kuthiwa kuphambene newashi futhi kwesokudla kwe-circularly polarized (RHCP). Uma inkambu izungeziswe ngendlela yewashi, inkambu izoba yi-circular polarization (LHCP) yesandla sobunxele.
I-elliptical polarization
Uma inkambu kagesi inezingxenye ezimbili ze-perpendicular, ama-degree angu-90 ngaphandle kwesigaba kodwa ngobukhulu obulinganayo, insimu izokwenziwa i-elliptically polarized. Uma kucatshangelwa indawo kagesi yegagasi lendiza elihamba libheke +z, elichazwe yi-Equation (4):
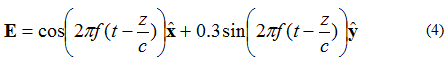
Indawo yephuzu lapho ichopho le-vector yenkundla kagesi izothatha khona inikezwe kuMfanekiso 5.
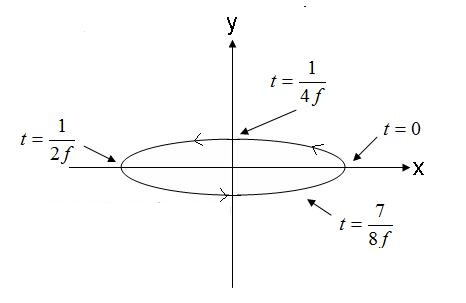
Umfanekiso 5. Inkambu kagesi esheshayo ye-elliptical polarization. (4).
Inkambu ekuMfanekiso 5, ehamba ngendlela ephambene newashi, izoba yi-elliptical esandleni sokudla uma iphuma esikrinini. Uma i-vector yenkundla kagesi izungeza ibheke kolunye uhlangothi, inkambu izokwenziwa i-elliptically polarized kwesokunxele.
Ngaphezu kwalokho, i-elliptical polarization ibhekisela eccentricity yayo. Isilinganiso se-eccentricity ku-amplitude yama-eksisi amakhulu namancane. Isibonelo, i-wave eccentricity esuka kusibalo (4) ingu-1/0.3= 3.33. Amagagasi e-elliptically polarized aphinde achazwe ngokuqondiswa kwe-eksisi enkulu. Isibalo segagasi (4) sine-eksisi ngokuyinhloko ehlanganisa i-eksisi ka-x. Qaphela ukuthi i-eksisi enkulu ingaba kunoma iyiphi i-engeli yendiza. I-engeli ayidingekile ukuze ilingane i-eksisi X, Y noma Z. Okokugcina, kubalulekile ukuqaphela ukuthi kokubili i-polarization eyindilinga kanye ne-linear yizimo ezikhethekile ze-elliptical polarization. Igagasi eliyi-eccentric elliptically polarized igagasi eliyindilinga eliyindilinga. Amagagasi e-elliptically polarized ane-eccentricity engapheli. Amagagasi ane-polarized.
I-antenna polarization
Manje njengoba sesizazi ngezinkambu ze-electromagnetic wave wave plane, i-polarization ye-antenna ichazwa kalula.
I-Antenna Polarization Ukuhlola kwenkundla ekude ye-antenna, ukuhlukaniswa kwenkambu ewumphumela yemisebe. Ngakho-ke, ama-antenna avame ukufakwa ohlwini "njenge-polarized linearly" noma "ama-antenna ayisiyingi asesandleni sokudla".
Lo mqondo olula ubalulekile ekuxhumaneni kwe-antenna. Okokuqala, i-antenna evundlile ene-polarized ngeke ixhumane ne-polarized antenna. Ngenxa ye-theorem yokubuyelana, uthi ludlulisa futhi lwamukele ngendlela efanayo. Ngakho-ke, ama-antenna aqonde mpo adlulisa futhi amukele izinkambu eziqondile. Ngakho-ke, uma uzama ukudlulisa i-antenna ene-polarized polarized polarized, ngeke kube khona ukwamukela.
Esimweni esivamile, kuma-antenna amabili ahlukanisiwe azungeziswe ngokuhlobene ne-engeli ( ), ukulahleka kwamandla ngenxa yalokhu kungafani kwe-polarization kuzochazwa yi-polarization loss factor (PLF):
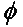
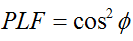
Ngakho-ke, uma izimpondo ezimbili zine-polarization efanayo, i-engeli phakathi kwezinkambu zama-electron akhipha imisebe inguziro futhi akukho ukulahleka kwamandla ngenxa yokungafani kwe-polarization. Uma uthi olulodwa lwenziwe i-polarized futhi olunye luvundlile, i-engeli ingama-degree angu-90, futhi awekho amandla azodluliswa.
QAPHELA: Ukuhambisa ifoni phezu kwekhanda lakho iye engeli ehlukene kuchaza ukuthi kungani ukwamukela ngezinye izikhathi kungase kwandiswe. Izimpondo zocingo ngokuvamile zihlukaniswa ngokwemigqa, ngakho-ke ukuzungezisa ifoni ngokuvamile kungase kuhambisane nokwehluka kwefoni, ngaleyo ndlela kuthuthukisa ukwamukela.
I-polarization eyindilinga iyisici esifiselekayo sama-antenna amaningi. Womabili ama-antenna ane-polarized futhi awahlushwa ukulahlekelwa kwesignali ngenxa yokungafani kwe-polarization. Ama-antenna asetshenziswa ezinhlelweni ze-GPS ane-polarized kwesokudla kwesokudla.
Manje cabanga ukuthi i-antenna eyenziwe nge-polarized ithola amagagasi ayisiyingi. Ngokufanayo, cabanga ukuthi i-antenna eyisiyingi izama ukuthola amagagasi agqagqene. Iyini umphumela wokulahlekelwa kwe-polarization?
Khumbula ukuthi i-polarization eyindilinga empeleni ingamagagasi e-orthogonal e-polarized, ama-degree angama-90 ngaphandle kwesigaba. Ngakho-ke, i-antenna ye-linearly polarized (LP) izothola kuphela ingxenye yesigaba se-circularly polarized (CP). Ngakho-ke, i-antenna ye-LP izoba nokulahlekelwa kwe-polarization okungafani no-0.5 (-3dB). Lokhu kuyiqiniso kungakhathaliseki ukuthi i-antenna ye-LP izungeziswe ngayiphi i-engeli. ngakho-ke:
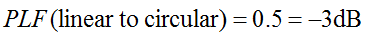
Isici sokulahlekelwa kwe-polarization kwesinye isikhathi sibizwa ngokuthi ukusebenza kahle kwe-polarization, i-antenna mismatch factor, noma into yokwamukela i-antenna. Wonke la magama abhekisela emcabangweni ofanayo.
Isikhathi sokuthumela: Dec-22-2023







